【算法】买卖股票的最佳时间系列问题

Posted on | In | Visitors:

买卖股票系列问题是LeetCode上一个很经典的系列问题，问题由浅入深，很有意思。这些问题当中，最简单的场景只需要对数组进行一次遍历并将极值求出即可，而复杂的场景则需要应用到动态规划思想去求解。

简单场景显然不是本文讨论的重点，但是我们需要通过简单场景，理解其中的动态规划思想，然后解答复杂场景的难题。

题目简述

买卖股票系列问题的核心是：

1
2
给与某支股票若干天内的价格序列，问如何买卖股票能获得最大收益。
例如，某支股票在连续6天内价格分别为 [7， 1， 5， 3， 6， 4] ，问在哪天买入，哪天卖出，能够获得最大收益（卖出必须在买入之后）

该系列问题一共有6个场景，分别有不同的买卖操作要求和限制，具体如下：

LeetCode题目序号 题目 要点概述
121 买卖股票的最佳时机 一次买卖，取最大利润
122 买卖股票的最佳时机 II 不限买卖次数
714 买卖股票的最佳时机-含手续费 不限买卖次数，但是每次卖出股票需要付手续费
309 买卖股票的最佳时机-含冷冻期 不限买卖次数，但是每次卖出需要等1天才能再次买入
123 买卖股票的最佳时机 III 最多买卖2次
188 买卖股票的最佳时机 IV 最多买卖 k 次

DP 思路解析

动态规划思想回顾

回顾一下动态规划的思想。用一个经典的入门级动态规划问题 斐波拉契数列 来回顾一下。

对于 斐波拉契数列 的第 i 项，总可以由以下公式递归得出：

1
2
Fibonacci(i) = Fibonacci(i - 1) + Fibonacci(i - 2)
# 为了便于行文，以下 Fibonacci(i) 函数简写为 F(i)

而在递归过程中，总有一些状态能提前碰到。比如计算第6项时， F(6) = F(5) + F(4)，我们能得到第 5 项和第 4 项 的值，而计算第 7 项， F(7) = F(6) + F(5)，有需要计算第 6 项和第 5 项。

因此，我们在计算 F(6) 时就将 F(6) 和 F(5) 的值记录下来；在计算 F(7) 时直接用上之前的值，就不用再重复计算了。

所以，递推和记录就构成了动态规划思想的核心。而动态规划用于解题，关键就是要找到这个状态转移方程式，即上面提到的递推公式。

至于什么问题可以由动态规划的思想得出呢？需要满足：

  1. 重叠子问题：即可以通过记录的方式避免重复求解子问题
  2. 无后向性：子问题的结果不影响后续问题的解
买卖股票的动态规划思路

本题中需要对数据的操作有2种：买入和卖出。如果只有一个状态，那就很难找到状态的转移过程了。但是，如果

  1. 将状态分为 “持有股票” 和 “不持有股票”，分别对2种状态计算最大收益；
  2. 利用负收益来记录持有股票状态，把买入动作造成的成本也记录进来
    可以发现：第 i 天的 “持有股票” 和 “不持有股票” 的状态均可以由前一天对应的状态转化过来，并且不会影响后续状态。

这种思路竟然很巧妙的符合了动态规划解题的2个要求。

具体如下：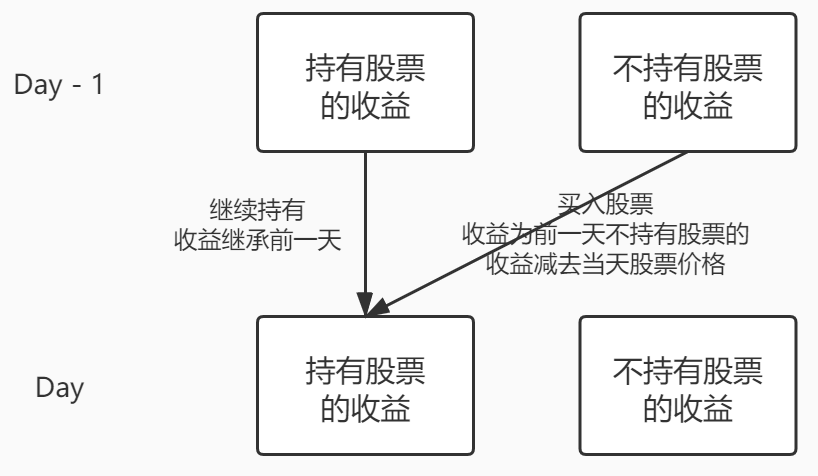
“持有股票” 状态转移

对于持有股票的状态，它可以由前一天的2种状态转移过来：

  1. 如果前一天就持有股票，则继承它的收益（不进行买入操作，收益不变）
  2. 如果前一天不持有股票，则需要按前一天不持有股票状态的收益，减去当前股票价格，可以理解为按今天的价格买入股票

对于上面的第2种情况，如果在系列问题场景一中，即只买卖一次的情况下，则只能由 0 收益转移过来。因为只交易一次，它的前一天一定是没有进行过交易，那么收益和成本均为0。

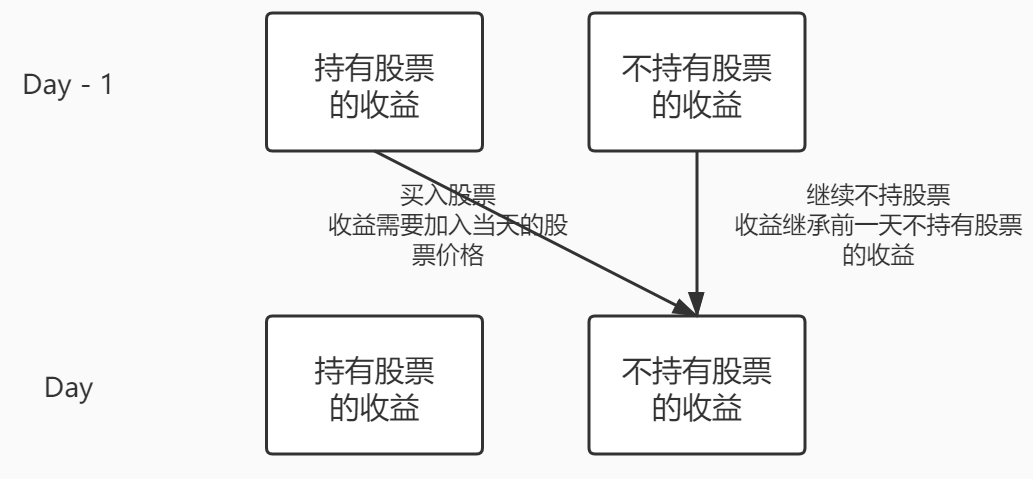
“不持有股票” 状态转移

对于不持有股票的状态，它也可以由前一天的2种状态转移过来：

  1. 如果前一天持有股票，今天卖出股票，则可以按照当天股价进行收割，计算当前收益
  2. 如果前一天也不持有股票，则继承昨天的收益，因为不买不买，不亏不赚

大致介绍了动态规划的思路，接下来我们就具体的场景，带入动态规划的解题思想，对不同场景的问题各个击破。

基本型：一次买卖

题目分析

此场景其实不需要动态规划，只需要遍历 prices 数组时，记录之前的股票最低价，同时计算当前抛出股票的收益；遍历过程取最大值即可。因为不能先卖再买，所以不用算后面出现的更低价。伪代码如下：

1
2
3
4
5
6
7
minPrice <- Integer.MAX_VALUE
maxProfit <- 0
for day in days:
    if prices[day] < minPrice:
        minPrice <- prices[day]
    curProfit <- prices[day] - minPrice
    maxProfit <- MAX{curProfit, maxProfit}

讨论这种解法不是本文的目的，我们的目的是为了更容易理解后续变种的解法，所以尝试用DP的思想来解这道题。

状态转移方程

经过前面对动态规划思想的分析，此处直接给出状态转移方程式：

1
2
 Hold(i)   = Max{ Hold(i-1),    0 - prices[i] }
NotHold(i) = Max{ NotHold(i-1), Hold(i-1) + prices[i] }

  • Hold 函数 表示第 i 天时，手上持有股票所累积的收益，或者说成本。它由 2 种状态转移过来：
    • 情况 1： 前一天已经持有股票，这时直接继承前一天的收益（或成本）
    • 情况 2： 今天买入股票，那么成本为 -prices[i]
  • NotHold 函数 表示第 i 天时，手上不持有股票所积累的收益。它也由 2 种状态转移过来：
    • 情况 1： 前一天没有持有股票，则收益继承；
    • 情况 2： 将前一天的股票卖出，收益为 prices[i] - Hold(i-1)

本质上，Hold 函数是用于计算第 i 天之前，股票最低价格是多少；而 NotHold 函数则用于计算如果今天卖出股票，可以收益多少钱。

填表过程

以股价 [7， 1， 5， 3， 6， 4] 为例：

天数 股价 Hold NotHold
1 7 -7 0
2 1 Max{ Hold(1), 0 - prices[2] }
= Max{ -7, 0 - 1 }
= -1		 Max{ NotHold(1), Hold(1) + prices[2] }
= Max{ 0, 1 + (-7) }
= 0
3 5 Max{ Hold(2), 0 - prices[3] }
= Max{ -1, 0 - 5 }
= -1		 Max{ NotHold(2), Hold(2) + prices[3] }
= Max{ 0, 5 + (-1) }
= 4
4 3 Max{ Hold(3), 0 - prices[4] }
= Max{ -1, 0 - 3 }
= -1		 Max{ NotHold(3), Hold(3) + prices[4] }
= Max{ 4, 3 + (-1) }
= 4
5 6 Max{ Hold(4), 0 - prices[5] }
= Max{ -1, 0 - 6 }
= -1		 Max{ NotHold(4), Hold(4) + prices[5] }
= Max{ 4, 6 + (-1) }
= 5
6 4 Max{ Hold(5), 0 - prices[6] }
= Max{ -1, 0 - 4 }
= -1		 Max{ NotHold(5), Hold(5) + prices[6] }
= Max{ 5, 4 + (-1) }
= 5

可以看到，NotHold(6) 的结果为 5，表示第 6 天不持有股票（已经卖出）的最大收益为 5。

其他分析
  • Question：为什么 NotHold 第二个状态的由来是 Hold(i-1) + prices[i] ？
  • Answer：第二个状态表示今天以prices[i]的价格卖出股票，而 Hold(i-1) 表示前一天持有股票的最大收益（成本最小）

P.S. 其实这个 “只进行一次买卖” 的场景下，Hold 函数其实就是找到成本最低的那一天进行买入。

理想量化交易：不限买卖次数

题目分析

此场景不限制交易次数，意味着只要找到每次涨跌的极值，进行扣除计算，就能算出最大利润。但是这种算法依然不是本篇讨论的重点。

在 DP 思路的框架下，对于 Hold 函数，如果由 情况2（今天才买入股票）转移过来，则它的收益应该是昨天未持有股票的收益，扣除今天买入股票的成本。

CAUTION：这个场景是 DP 思路的关键；理解了这个场景，后续场景更难的问题，理解起来就容易得多。

状态转移方程

同样，直接给出状态转移方程：

1
2
 Hold(i)   = Max{ Hold(i-1),    NotHold(i-1) - prices[i] }
NotHold(i) = Max{ NotHold(i-1), Hold(i-1) + prices[i] }

Question：为什么 Hold 函数可以从 NotHold(i-1) - prices[i] 转移来？如果减去当天的估价，不是肯定会比 Hold(i-1) 低么；如果 Hold(i-1) 永远大于 NotHold(i-1) - prices[i]，那么不是永远不会从 NotHold 转移过来了？

Answer：需要了解，如果 Hold 从 NotHold(i-1) 转移过来，那么 NotHold(i-1) 已经将 Hold(i-2) 的利益收割了。比如下面这种情况（假设最初股票为1元）：

天数 股价 Hold NotHold
1 1 -1 0
2 3 -1
（继续持有）		 2
（卖出股票，收割 2 元）
3 2 0
（由 NotHold(2) 转移过来，已经将收割的 2 元计算进来了）		 2
（虽然按今天的估价卖出能赚 1 元，但显然不如昨天卖出股票收益大）
填表过程

依然以股价 [7， 1， 5， 3， 6， 4] 为例：

天数 股价 Hold NotHold
1 7 -7 0
2 1 Max{ Hold(1), NotHold(1) - prices[2] }
= Max{ -7, 0 - 1 }
= -1
（今天买入更划算）		 Max{ NotHold(1), Hold(1) + prices[2] }
= Max{ 0, 1 + (-7) }
= 0
（昨天买今天卖还亏了6块，不如空仓）
3 5 Max{ Hold(2), NotHold(2) - prices[3] }
= Max{ -1, 0 - 5 }
= -1
（昨天空仓今天再买入，花了5块，不如昨天1元买入，今天继续按昨天的成本持有）		 Max{ NotHold(2), Hold(2) + prices[3] }
= Max{ 0, 5 + (-1) }
= 4
(昨天1元买入，今天5元卖出，肯定比持续空仓划算)
4 3 Max{ Hold(3), NotHold(3) - prices[4] }
= Max{ -1, 4 - 3 }
= 1
（前天1元买入，收益为-1；如果昨天卖了一手，今天再买，收益为1了）		 Max{ NotHold(3), Hold(3) + prices[4] }
= Max{ 4, 3 + (-1) }
= 4
（如果按前天1元的成本买入，今天3块卖出，赚2块；但是昨天5块卖出，今天保持空仓，收益为4块）
5 6 Max{ Hold(4), NotHold(4) - prices[5] }
= Max{ 1, 4 - 6 }
= 1
（按昨天收益继续持有，还是昨天卖出今天重新买入？显然保持昨天收益更高）		 Max{ NotHold(4), Hold(4) + prices[5] }
= Max{ 4, 6 + 1 }
= 7
（昨天持仓的收益为1，按照今天的价格卖出能再赚6块）
6 4 Max{ Hold(5), NotHold(5) - prices[6] }
= Max{ 1, 7 - 4 }
= 3		 Max{ NotHold(5), Hold(5) + prices[6] }
= Max{ 7, 1 + 4 }
= 5

现实量化交易：不限买卖次数，但是每次卖出需要收手续费

题目分析

此种场景既是上一种场景（理想量化交易）的升级版，也是为什么一定要用 DP 思想来解这道题的原因。之前两种场景，无论是只进行1次交易，或者不限制交易次数，采用最大值、递增子序列等方法都能完成题目的解答。但是从这种场景开始，初阶解法在股票买卖场景中变得不适用了。

来聊聊解法吧。可以发现，在不限制交易的场景中，把状态方程稍作变更，就能解这道题了。具体的，在 NotHold 函数中，如果今天决定将股票卖出，那么我们再扣除一部分固定的交易费即可。

状态转移方程
1
2
 Hold(i)   = Max{ Hold(i-1),    NotHold(i-1) - prices[i] }
NotHold(i) = Max{ NotHold(i-1), Hold(i-1) + prices[i] - fee }

变更很简单，其实就是不限交易场景中，每次卖出股票再交一笔费用。

填表过程

以股价 [1, 3, 2, 8, 4, 9] ，交易费为 2 为例

天数 股价 Hold NotHold
1 1 -1 0
2 3 Max{ Hold(1), NotHold(1) - prices[2] }
= Max{ -1, 0 - 3 }
= -1		 Max{ NotHold(1), Hold(1) + prices[2] - fee }
= Max{ 0, 3 + (-1) - 2 }
= 0
3 2 Max{ Hold(2), NotHold(2) - prices[3] }
= Max{ -1, 0 - 2 }
= -1		 Max{ NotHold(2), Hold(2) + prices[3] - fee }
= Max{ 0, 2 + (-1) - 2}
= 0
4 8 Max{ Hold(3), NotHold(3) - prices[4] }
= Max{ -1, 0 - 8 }
= -1		 Max{ NotHold(3), Hold(3) + prices[4] - fee }
= Max{ 0, 8 + (-1) - 2}
= 5
5 4 Max{ Hold(4), NotHold(4) - prices[5] }
= Max{ -1, 5 - 4 }
= 1		 Max{ NotHold(4), Hold(4) + prices[5] - fee }
= Max{ 5, 4 + (-1) - 2}
= 5
6 9 Max{ Hold(5), NotHold(5) - prices[6] }
= Max{ 1, 5 - 9 }
= 1		 Max{ NotHold(5), Hold(5) + prices[6] - fee }
= Max{ 5, 9 + 1 - 2}
= 8

因此，最大收益为 8.

风险控制型：卖出后 1 天有冷冻期

题目分析

此场景和上面2种场景很相似，具体处理在 Hold 函数的状态转移时，取前天的 NotHold 值，而不是取昨天的。

状态转移方程
1
2
 Hold(i)   = Max{ Hold(i-1),    NotHold(i-2) - prices[i] }
NotHold(i) = Max{ NotHold(i-1), Hold(i-1) + prices[i] }

自律型：只买卖 2 次 / 只买卖 k 次

题目分析

这两种场景在状态转移上差别不大。看起来限制交易 2次的场景比 k次场景更简单，但如果用 DP 的思想求解，其实是一致的。
P.S. 如果不用DP，暴力求解，2次场景是能过的

需要注意的有3点：

  1. 由于限制了最大交易次数，所以需要记录以前发生了多少次交易
  2. 很有可能最大利润不需要完成最大交易次数，就比如股价如果为 [1, 2, 3, 4, 5]，为了收益最大化，其实只能进行 1 次交易
  3. 由于买需要1天，卖需要1天，所以最大交易次数其实为 prices.length / 2
状态转移方程

因为限制了最大交易次数，需要记录已经发生的交易次数，这一点需要体现在状态转移方程中。

具体的：

1
2
 Hold(k, i)   = Max{ Hold(k, i-1),    NotHold(k - 1, i-1) - prices[i] }
NotHold(k, i) = Max{ NotHold(k, i-1), Hold(k, i-1) + prices[i] }

我们增加一个 k 变量到 Hold 和 NotHold 中，表示：

  • Hold(k, i)： 第 i 天，已经交易 k 次（包括今天买入这一次），持有股票的最大利润；它的转移情况：
    • 情况 1： 前一天已经持有股票，这时直接继承前一天的收益（或成本），此时交易次数 k 不变
    • 情况 2： 今天买入股票，那么收益为昨天不持有股票的状态减去今天的估价，并且昨天的交易次数是 k - 1
  • NotHold(k, i)：第 i 天，已经交易 k 次（如果今天卖出，其实交易次数不变），持有股票的最大利润
    • 情况 1： 前一天没有持有股票，继承昨天收益，且交易次数 k 不变；
    • 情况 2： 按今天股价将股票卖出，收益为 prices[i] - Hold(k, i-1)；由于买卖算作一次完整交易，故交易次数 k 不变
填表过程

以股价 [3, 2, 6, 5, 0, 3]，最大交易次数 k = 2 为例

天数 股价 Hold(0, i) NotHold(0, i) Hold(1, i) NotHold(1, i) Hold(2, i) NotHold(2, i)
1 3 0 0 -3 -∞ -∞ -∞
2 2 0 0 Max{-3, 0 - 2}
= -2		 Max{0, -∞ + (-3)}
= 0		 -∞
(当前第2天，不可能开始进行第 2 次交易)		 -∞
(当前第2天，不可能开始进行第 2 次交易)
3 6 0 0 Max{-2, 0 - 6}
= -2		 Max{0, 6 + (-2)}
= 4		 Max{-∞, 0 - 6}
= -6		 -∞
(当前第3天，不可能开始进行第 2 次，且能卖出股票)
4 5 0 0 Max{-2, 0 - 5}
= -2		 Max{4, 5 + (-2)}
= 4		 Max{-6, 4 - 5}
= -1		 Max{-∞, 5 + (-6)}
= -1
5 0 0 0 Max{-2, 0 - 0}
= 0		 Max{4, 0 + (-2)}
= 4		 Max{-1, 4 - 0}
= 4		 Max{-1, 0 + -1}
= -1
6 3 0 0 Max{0, 0 - 3}
= 0		 Max{4, 3 + (-0)}
= 4		 Max{4, 4 - 3}
= 4		 Max{-1, 3 + 4}
= 7

注意事项：

  1. Hold(0, 1) 和 NotHold(0, i) 都是无意义的，因为进行 0 次交易，收益永远是 0
  2. 初始化：只有 Hold(1, 0) 需要初始化为 -prices[0]，Hold(k, i)、NotHold(k, i) (k > 1) 最好都初始化为 -∞
  3. 交易合理性：递推的过程中判断当前状态是否可达，比如第 2 天时，最多只可能进行1次交易（第1天买，第2天卖），Hold(2, 2) 是不可达的；同理，第 3 天时，NotHold(2, 3) 也是不可达的
  4. 降维处理：对于 Hold 和 NotHold，它们其实只依赖前一天对应的状态，因此没必要申请一个 days × k 的二维表，相关算法可参考 DP 思路下的斐波拉契数列；其他场景也可进行降维优化，但最大 k 次交易的场景下，如果不进行降维优化，很可能超出内存限制

结语

以上。

References

  1. 「leetcode」买卖股票的最佳时机I、II、III、IV、含手续费、含冷冻期
  2. （英文原文）Most consistent ways of dealing with the series of stock problems
0%