Leetcode_901-Outline Stock Span

Posted on | In | Visitors:

题目介绍

简而言之，是给定一串数字，要求输出最长连续递增子序列的长度。

Write a class StockSpanner which collects daily price quotes for some stock, and returns the span of that stock’s price for the current day.

The span of the stock’s price today is defined as the maximum number of consecutive days (starting from today and going backwards) for which the price of the stock was less than or equal to today’s price.

For example, if the price of a stock over the next 7 days were [100, 80, 60, 70, 60, 75, 85], then the stock spans would be [1, 1, 1, 2, 1, 4, 6].


Trial：二分搜索

思路：

  1. 找最长递增子序列，其实就是找第一个大于当前值的price的出现位置
  2. 按时间记录所有股价，然后每次从mid出发，先往后找，再往前找，寻找第一个出现的larger值

结局：超时

正解：递减栈

查找资料，网上的解法，构造一个严格递减的栈（栈顶price > 栈底price），并用另一个数组记录小于栈内对应price的次数。然后每次拿到新的newPrice，从栈顶往下数，小于newPrice
的出栈，并记录数量sum；直到找到第一个大于newPrice
，然后将newPrice以及对应次数入栈。

思路图解：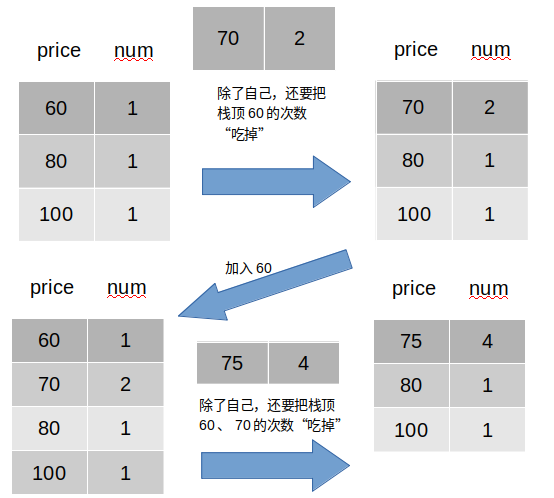
image
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class StockSpanner{

    private static final int[] priceStack = new int[10000];
    private static final int[] daysStack = new int[10000];
    private int stackLen;

    public StockSpanner(){
        this.stackLen = 0;
        priceStack[0] = -1;
        daysStack[0] = 0;
    }

    public int next(int price){

        int daySum = 1;
        while (this.stackLen >= 0){
            if (priceStack[this.stackLen] <= price){
                daySum += daysStack[this.stackLen];
            }else{
                break;
            }
            this.stackLen --;
        }
        priceStack[++this.stackLen] = price;
        daysStack[this.stackLen] = daySum;

        return daySum;
    }
}

其他解法

根据参考资料[2]，可尝试使用DP求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// Author: Huahua, 144 ms
class StockSpanner {
public:
  StockSpanner() {}
 
  int next(int price) {
    if (prices_.empty() || price < prices_.back()) {
      dp_.push_back(1);      
    } else {
      int j = prices_.size() - 1;
      while (j >= 0 && price >= prices_[j]) {
        j -= dp_[j];
      }
      dp_.push_back(prices_.size() - j);
    }    
    prices_.push_back(price);    
    return dp_.back();
  }
private:
  vector<int> dp_;
  vector<int> prices_;  
};

基本思路：找到第一个大于当前值的参数位置
技巧：如果 price[j-1] <= price[j]，那么向前移动的距离为 dp[i-1]（即第i-1个数的最长连续递增序列长度），这样就缩短了寻找的路程
思考方式：寻找状态转移之间的关系

弯路（WARNING： 只是记录一些可能有价值的思路，非本题正解）

第一次读题，我以为是找历史上小于等于当天股价的天数。于是想，如果维护一个有序数组，记录每天股价；当读取新一个股价，对小于它股价的出现次数进行一波求和，不就解决问题了：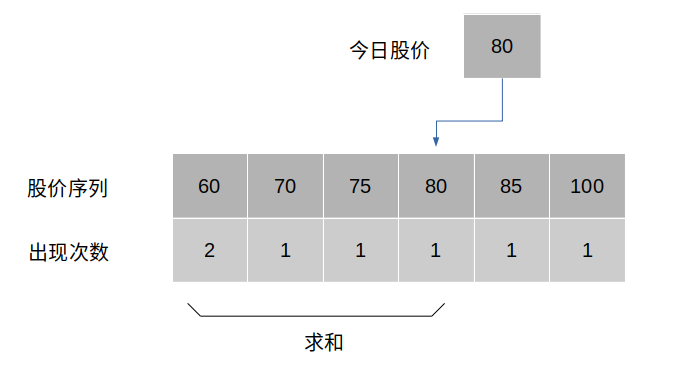
image
于是想，这个题应该可以用平衡树AVL来解决。每个节点记录：

  1. 本节点price
  2. price出现的次数
  3. 左右子树的共同次数（便于AVL旋转时变更统计数量）

然后每次只需要统计当前节点的次数以及左子树的所有次数。结构如图：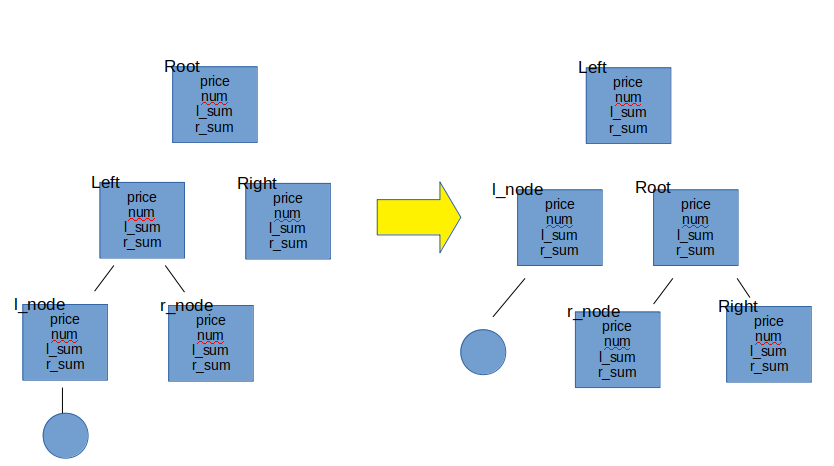
image
以右旋为例，除了进行常规节点变更操作（此处不赘述），还进行左右子树数量调整：

  1. Root->l_sum = r_node.totalSum() (r_node 的子节点没变，可直接复赋值)
  2. Left->r_sum = Root.totalSum()

然后每次获取新值，只需要返回 node->num + node->l_sum 即可。
然而题目并不是这个意思。所以先将思路记录下来，以后遇到类似的题目，可以类比搜索一下，验证正确性，并检索更优解法。

0%